동차 좌표, 어파인 공간, 어파인 변환: 이동, 회전, 스케일, 밀림 변환

1. 어파인 공간과 기초 개념

그래픽스에서는 위치를 나타내는 점(Point) 과 방향과 크기를 나타내는 벡터(Vector) 를 명확히 구분합니다.

📌 벡터 연산

벡터는 방향과 크기를 가지는 물리적인 양이며, 보통 화살표로 표현합니다.

두 벡터 ( \vec{a} = (a_1, a_2) ), ( \vec{b} = (b_1, b_2) )에 대해: 합: ( \vec{a} + \vec{b} = (a_1 + b_1, a_2 + b_2) )차: ( \vec{a} - \vec{b} = (a_1 - b_1, a_2 - b_2) )상수배: ( c\vec{a} = (c a_1, c a_2) )

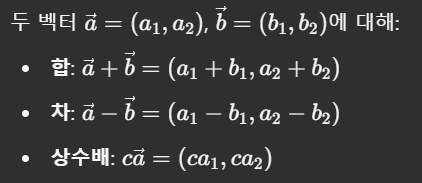
📌 점과 벡터 연산

점 ( P = (x, y) ), 벡터 ( \vec{v} = (v_x, v_y) )일 때:점 + 벡터 = 점: ( P + \vec{v} = (x + v_x, y + v_y) )점 - 점 = 벡터: 두 점 ( A, B )에 대해 ( \vec{v} = B - A )

• ❗ 점 + 점은 수학적으로 정의되지 않음: 위치 간의 덧셈은 의미 없음

---

2. 어파인 결합과 좌표계

📌 어파인 결합이란?

어파인 결합은 여러 점 또는 벡터를 선형 결합한 것으로, 계수의 합이 1인 경우 점을, 0인 경우 벡터를 생성합니다. 다음 수식처럼 표현할 수 있습니다:

[ \sum_{i=1}^{n} \alpha_i p_i = \alpha_1 p_1 + \alpha_2 p_2 + \cdots + \alpha_n p_n, \quad \text{where } \sum_{i=1}^{n} \alpha_i = 1 \text{ or } 0 ]

( \sum \alpha_i = 1 ) → 결과는 점( \sum \alpha_i = 0 ) → 결과는 벡터

예시 수식을 통해 자세히 보면:

[\alpha_1 p_1 + \alpha_2 p_2 + \alpha_3 p_3 = (\alpha_1 + \alpha_2 + \alpha_3)p_1 + \alpha_2(p_2 - p_1) + \alpha_3(p_3 - p_1)= (\alpha_1 + \alpha_2 + \alpha_3)p_1 + \alpha_2 \vec{u} + \alpha_3 \vec{v}] 이때 ( \vec{u} = p_2 - p_1 ), ( \vec{v} = p_3 - p_1 )( \alpha_1 + \alpha_2 + \alpha_3 = 1 )이면 결과는 점, 0이면 벡터

📌 n차원 어파인 좌표계

어파인 공간에서는 기준점(origin) 과 기저 벡터(basis vectors) 로 좌표계를 정의합니다.

n차원 어파인 공간에서는:

기준점 ( o )n개의 방향 벡터 ( \vec{v}_1, \vec{v}_2, \dots, \vec{v}_n )어파인 좌표계 ( F = [\vec{v}_1 \ \vec{v}_2 \ \cdots \ \vec{v}_n \ o] )

3차원 예시에서는 다음과 같이 표현됩니다:

기준점 ( o )축 벡터 ( \vec{v}_1, \vec{v}_2, \vec{v}_3 )임의의 점 ( p )는:[p = o + x \vec{v}_1 + y \vec{v}_2 + z \vec{v}_3]

이 표현 방식은 점과 벡터의 본질적인 차이를 명확하게 해줍니다. (벡터는 원점과 무관하지만, 점은 원점 기준으로 위치를 정함)

---

3. 동차(Homogeneous) 좌표와 그 필요성

📌 동차 좌표란?

일반적인 2D 점 ( (x, y) ) → 동차 좌표로 ( (x, y, 1) )벡터 ( (v_x, v_y) ) → 동차 좌표로 ( (v_x, v_y, 0) )

📌 왜 동차 좌표를 사용하는가?

일반적인 선형 변환 행렬은 이동(translation)을 포함할 수 없습니다. 그러나 동차 좌표를 사용하면 이동까지도 행렬 곱으로 표현할 수 있습니다.

이 방식은 OpenGL이나 행렬 기반 그래픽 시스템에서 필수적입니다. 예:

일반 좌표: ( (x, y) + (t_x, t_y) )동차 좌표: 행렬 곱으로 표현 가능:[\begin{bmatrix} 1 & 0 & t_x \ 0 & 1 & t_y \ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \ y \ 1 \end{bmatrix}]

❗ 점 + 점이 정의되지 않는 이유 (동차 좌표 관점)

동차 좌표에서 점은 ( (x, y, 1) ), 벡터는 ( (v_x, v_y, 0) )입니다. 점 + 점을 하면 마지막 좌표 값이 ( 1 + 1 = 2 )가 되어 점인지 벡터인지 구분할 수 없게 되어 수학적으로 무의미합니다. 반면 점 - 점 = 벡터는 ( 1 - 1 = 0 )이 되어 정상적인 벡터로 해석됩니다.

---

4. 어파인 변환과 행렬 표현

📌 어파인 변환이란?

어파인 변환은 직선성(linearity)을 유지하는 변환으로, 벡터의 평행성, 직선의 보존, 비율 유지 등의 특성을 가집니다. 일반적으로:

• 이동 (Translation)
• 회전 (Rotation)
• 스케일 (Scaling)
• 밀림 (Shearing)
  을 포함합니다.

📌 어파인 변환의 동차 행렬 표현

모든 어파인 변환은 동차 좌표를 사용해 3×3 행렬로 표현할 수 있습니다 (2D 기준).

예시 (이동 변환):

[ T = \begin{bmatrix} 1 & 0 & t_x \ 0 & 1 & t_y \ 0 & 0 & 1 \end{bmatrix} ]

이러한 형식은 변환들을 쉽게 행렬 곱으로 합성할 수 있게 해줍니다.

---

5. 기본 어파인 변환 종류

🔹 이동 (Translation)

🔹 2D의 경우

동차 좌표계를 사용하여 이동 변환을 행렬로 나타내면:

[ T = \begin{bmatrix} 1 & 0 & t_x \ 0 & 1 & t_y \ 0 & 0 & 1 \end{bmatrix} ]

🔹 3D의 경우

[ T = \begin{bmatrix} 1 & 0 & 0 & t_x \ 0 & 1 & 0 & t_y \ 0 & 0 & 1 & t_z \ 0 & 0 & 0 & 1 \end{bmatrix} ]

이 행렬의 오른쪽 마지막 열 ( (t_x, t_y, [t_z]) ) 성분이 바로 이동량입니다.

---

✍️ 실제로 계산해보기

🌟 점에 대한 이동 변환

점 ( p = (p_x, p_y) ) → 동차 좌표로 ( \begin{bmatrix} p_x \ p_y \ 1 \end{bmatrix} ) [T \cdot p =\begin{bmatrix}1 & 0 & t_x \0 & 1 & t_y \0 & 0 & 1\end{bmatrix}\cdot\begin{bmatrix}p_x \p_y \1\end{bmatrix}=\begin{bmatrix}p_x + t_x \p_y + t_y \1\end{bmatrix}]

➡️ 점은 정확히 원하는 만큼 이동함을 확인할 수 있어요!

---

🌟 벡터에 대한 이동 변환

벡터 ( \vec{v} = (v_x, v_y) ) → 동차 좌표로 ( \begin{bmatrix} v_x \ v_y \ 0 \end{bmatrix} ) [T \cdot \vec{v} =\begin{bmatrix}1 & 0 & t_x \0 & 1 & t_y \0 & 0 & 1\end{bmatrix}\cdot\begin{bmatrix}v_x \v_y \0\end{bmatrix}=\begin{bmatrix}v_x \v_y \0\end{bmatrix}= \vec{v}]

➡️ 벡터는 이동 변환의 영향을 전혀 받지 않음!

이유는 마지막 성분이 0이기 때문에, 행렬 곱에서 ( t_x, t_y ) 가 곱해질 일이 없기 때문이에요.

🔄 이동 변환의 역행렬

역행렬은 다음과 같이 간단합니다:

🔹 2D: [T^{-1} =\begin{bmatrix}1 & 0 & -t_x \0 & 1 & -t_y \0 & 0 & 1\end{bmatrix}] 🔹 3D: [T^{-1} =\begin{bmatrix}1 & 0 & 0 & -t_x \0 & 1 & 0 & -t_y \0 & 0 & 1 & -t_z \0 & 0 & 0 & 1\end{bmatrix}]

👉 이유: 원래 위치로 되돌리려면, 이동했던 거리만큼 반대로 이동하면 되기 때문이에요!

---

🧮 행렬 곱으로 확인해보기

직접 곱해보면:

[ T \cdot T^{-1} = \begin{bmatrix} 1 & 0 & t_x \ 0 & 1 & t_y \ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -t_x \ 0 & 1 & -t_y \ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{bmatrix} = I ]

➡️ 단위 행렬 ( I ) 이 되므로, 역행렬이 맞는 걸 알 수 있어요!

---

🔹 회전 (Rotation)

회전 변환은 어떤 기준점(보통은 원점)을 중심으로 객체(점, 벡터)를 일정 각도만큼 회전시키는 변환입니다.
이 변환은:

• 길이와 각도 유지
• 직선성과 평행성 유지
• 벡터와 점 모두 회전 대상이 될 수 있음

---

✅ 2. 2D 회전 변환 (z축 기준 회전)

🔹 회전 행렬

[ R(\theta) = \begin{bmatrix} \cosθ & -\sinθ & 0 \ \sinθ & \cosθ & 0 \ 0 & 0 & 1 \end{bmatrix} ]

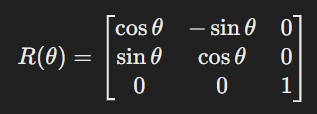
이 행렬은 원점을 기준으로 θ만큼 반시계 방향으로 회전합니다.

🔹 어떤 성분이 회전을 만드는가?

• 회전은 상위 2×2 블록의 cosθ, (sinθ 성분이 담당합니다.
• 이들은 x, y 좌표를 서로 섞어 바꾸는 방식으로 회전을 만들어냅니다.

🔹 실제 적용 예시

점 ( p = (x, y) ) → 동차 좌표로 ( (x, y, 1)^T ) [ R(\theta) \cdot \begin{bmatrix} x \ y \ 1 \end{bmatrix} = \begin{bmatrix} x\cosθ - y\sinθ \ x\sinθ + y\cosθ \ 1 \end{bmatrix} ]

➡️ 반시계 방향으로 회전한 새로운 위치가 됩니다.

---

✅ 3. 3D 회전 변환 (원점 기준)

3D에서는 회전 축이 3가지로 나뉘고, 각 축에 대한 회전 행렬이 다릅니다.

🔹 x축 기준 회전 (y–z 평면에서 회전)

[ R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & \cosθ & -\sinθ & 0 \ 0 & \sinθ & \cosθ & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ]

➡️ y와 z 좌표만 변하고, x는 그대로 유지됩니다.

---

🔹 y축 기준 회전 (x–z 평면에서 회전)

[ R_y(\theta) = \begin{bmatrix} \cosθ & 0 & \sinθ & 0 \ 0 & 1 & 0 & 0 \ -\sinθ & 0 & \cosθ & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ]

➡️ x와 z 좌표가 섞이고, y는 그대로 유지됩니다.

💥 주의할 점:

• x축 회전에서는 -sinθ가 아래에 나오지만
• y축 회전에서는 -sinθ가 왼쪽 위로 이동합니다.
• 👉 부호 위치가 달라지므로 주의!

---

🔹 z축 기준 회전 (x–y 평면에서 회전)

[ R_z(\theta) = \begin{bmatrix} \cosθ & -\sinθ & 0 & 0 \ \sinθ & \cosθ & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ]

➡️ x와 y 좌표가 바뀌고, z는 고정됩니다.
→ 2D 회전 행렬과 구조가 거의 동일해요.

---

✅ 4. 왜 부호가 다를까? — 오른손 법칙(Right-Hand Rule)

회전 방향은 단순히 수학적 convention이 아니라, 오른손 법칙에 따라 결정됩니다.

🖐 오른손 법칙이란?

1. 오른손 엄지를 회전축 방향으로 뻗습니다.
2. 나머지 손가락을 구부리는 방향이 양의 회전 방향입니다.

예시:

• 엄지를 z축 위로 → x–y 평면에서 반시계 방향 회전
• 엄지를 y축 앞쪽으로 → x–z 평면에서 z→x 방향으로 회전
• 그래서 y축 기준 회전은 -sinθ와 sinθ의 위치가 바뀜 → 부호 위치 달라짐

---

🎯 임의 축에 대한 회전 변환이란?

우리는 지금까지 x축, y축, z축을 중심으로 도는 회전만 배웠지만,
현실에서는 물체가 임의의 방향(예: 대각선 방향)으로도 회전할 수 있어야 하죠.

그래서 어떤 단위벡터 ( \vec{u} = (u_x, u_y, u_z) ) 를 축으로 해서,
각도 θ만큼 회전하는 행렬이 필요합니다.

---

✅ 수식 정리

회전 축:

[ \vec{u} = (u_x, u_y, u_z), \quad ❘\vec{u}❘ = 1 ]

회전 각도:

θ (radian)

---

📌 임의 축 회전 행렬 공식:

[R(\vec{u}, \theta) =(I - K) \cdot (1 - \cosθ) + K \cdot \sinθ + I \cdot \cosθ] 이걸 행렬 형태로 정리하면 아래와 같아요: [R(\vec{u}, \theta) =\begin{bmatrix}u_x^2 & u_x u_y & u_x u_z \u_y u_x & u_y^2 & u_y u_z \u_z u_x & u_z u_y & u_z^2\end{bmatrix} (1 - \cosθ) +\begin{bmatrix}0 & -u_z & u_y \u_z & 0 & -u_x \-u_y & u_x & 0\end{bmatrix} \sinθ +\begin{bmatrix}1 & 0 & 0 \0 & 1 & 0 \0 & 0 & 1\end{bmatrix} \cosθ]

이 표현은 Rodrigues의 회전 공식이라고도 불러요.

---

🧠 의미 분석

이 공식은 3가지 성분의 합입니다:

항	의미	역할
I * cosθ	항등행렬 × 회전량	원래 방향 유지
K * sinθ	반대방향의 회전 기여	회전의 축에 수직인 성분 회전
(1 - cosθ)(vec{u} ⊗ vec{u}))	외적이 아닌 내적의 기여	축 방향으로 남는 부분 보정

---

🔷 1. 직교 행렬(Orthogonal Matrix)이란?

📌 정의

행렬 ( R )이 직교 행렬이라면 다음을 만족합니다: R^{-1} = R^T

즉, 역행렬이 전치(transpose) 와 같아요!

---

📌 직교 행렬의 특징

1. 각 행/열은 단위 벡터 (길이 = 1)
   → 예: ( cos^2(θ) + sin^2(θ) = 1 )
2. 행/열 벡터끼리는 서로 직교 (내적 = 0)
   → 예: ( cosθsinθ - sinθcosθ = 0 )
3. 직교 행렬을 곱하면 크기와 각도가 보존됨
   → 물체를 회전해도 형태가 유지됨!
4. 행렬식 = ±1
   • +1: 회전 행렬
   • −1: 반사 행렬

---

🔷 2. 회전 행렬은 직교 행렬이다

✅ 2D 회전 행렬 예시

[ R(θ) = \begin{bmatrix} \cosθ & -\sinθ & 0 \ \sinθ & \cosθ & 0 \ 0 & 0 & 1 \end{bmatrix} ]

이 행렬은 직교 행렬 조건을 만족합니다:

• 각 열 벡터는 단위 길이
• 서로 직교
• 전치가 역행렬

---

🔷 3. 회전 행렬의 역행렬

✅ 핵심 공식

[R^{-1}(θ) = R(-θ) = R^T(θ)]

즉:

• 역회전은 θ의 부호만 바꾸면 됨
• 전치 행렬을 구하면 곧 역행렬

---

✅ 2D 회전 역행렬

[ R^{-1}(θ) = \begin{bmatrix} \cos(-θ) & -\sin(-θ) & 0 \ \sin(-θ) & \cos(-θ) & 0 \ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \cosθ & \sinθ & 0 \ -\sinθ & \cosθ & 0 \ 0 & 0 & 1 \end{bmatrix} ]

→ 전치 행렬과 같은 결과!

---

✅ 3D 회전 역행렬

축별로 회전 역행렬을 보면:

🔹 x축 기준 회전 [R_x^{-1} =\begin{bmatrix}1 & 0 & 0 & 0 \0 & \cosθ & \sinθ & 0 \0 & -\sinθ & \cosθ & 0 \0 & 0 & 0 & 1\end{bmatrix}] 🔹 y축 기준 회전 [R_y^{-1} =\begin{bmatrix}\cosθ & 0 & -\sinθ & 0 \0 & 1 & 0 & 0 \\sinθ & 0 & \cosθ & 0 \0 & 0 & 0 & 1\end{bmatrix}] 🔹 z축 기준 회전 [R_z^{-1} =\begin{bmatrix}\cosθ & \sinθ & 0 & 0 \-\sinθ & \cosθ & 0 & 0 \0 & 0 & 1 & 0 \0 & 0 & 0 & 1\end{bmatrix}]

→ 모두 전치 행렬과 같다는 것을 확인할 수 있어요.

✨ 요약

항목	내용
직교 행렬	역행렬 = 전치행렬
회전 행렬	항상 직교 행렬이다
역회전	부호만 반대로 하면 됨

---

🔹 스케일 (Scaling)

스케일 변환은 객체의 크기를 늘리거나 줄이는 변환이에요.
x, y (또는 z) 방향으로 각각 다른 배율로 확대하거나 축소할 수 있습니다.

• 크기를 2배 키우는 건 ( s = 2 )
• 절반으로 줄이는 건 ( s = 0.5 )

---

✅ 2. 2D 스케일 변환

🔹 스케일 행렬

[ S = \begin{bmatrix} s_x & 0 & 0 \ 0 & s_y & 0 \ 0 & 0 & 1 \end{bmatrix} ]

여기서:

• ( s_x ): x축 방향 배율
• ( s_y ): y축 방향 배율

🔹 점/벡터에 적용

점 p = (x, y) 또는 벡터 vec{v} = (v_x, v_y)를 동차좌표로 나타내고 곱하면:

[ p' = S \cdot p = \begin{bmatrix} s_x x \ s_y y \ 1 \end{bmatrix}, \quad \vec{v}' = S \cdot \vec{v} = \begin{bmatrix} s_x v_x \ s_y v_y \ 0 \end{bmatrix} ]

➡️ 점이든 벡터든, 해당 축 방향으로 늘어나거나 줄어듭니다.

---

✅ 3. 3D 스케일 변환

🔹 4×4 동차 좌표 행렬

[ S = \begin{bmatrix} s_x & 0 & 0 & 0 \ 0 & s_y & 0 & 0 \ 0 & 0 & s_z & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ]

• ( s_x ), ( s_y ), ( s_z ): 각각 x, y, z 축 방향의 배율

---

✅ 4. 역 스케일 변환

스케일링의 역변환은 간단하게 1/s 를 곱하는 형태입니다.

2D 역변환: [S^{-1} =\begin{bmatrix}1/s_x & 0 & 0 \0 & 1/s_y & 0 \0 & 0 & 1\end{bmatrix}] 3D 역변환: [S^{-1} =\begin{bmatrix}1/s_x & 0 & 0 & 0 \0 & 1/s_y & 0 & 0 \0 & 0 & 1/s_z & 0 \0 & 0 & 0 & 1\end{bmatrix}]

---

📌 주의할 점

• 0으로 스케일하면?
  → 해당 방향으로 완전히 납작해짐(축소) → 되돌릴 수 없음 → 역행렬 존재하지 않음
• 스케일은 크기만 바꾸므로, 방향이나 각도는 보존되지 않음

---

✨ 정리

항목	설명
스케일 행렬	대각 성분에 각각 축 방향 배율
점과 벡터	모두 스케일의 영향을 받음
역변환	배율의 역수 곱

🔹 밀림 (Shearing)

한 축을 기준으로 다른 축이 기울어지는 변환입니다.

밀림 변환은 물체를 특정 축을 기준으로 기울이는 변환입니다.

• 마치 상자가 비스듬히 눕는 듯한 효과를 줘요.
• 모양은 변하지만, 각 꼭짓점 간의 평행 관계는 유지됩니다.

---

✅ 2. 2D 밀림 변환

🔹 밀림 행렬

x축 기준 밀림 (y좌표에 따라 x값이 밀림): [Sh_x =\begin{bmatrix}1 & a & 0 \0 & 1 & 0 \0 & 0 & 1\end{bmatrix}\quad \text{(a: y가 클수록 x방향으로 많이 밀림)}] y축 기준 밀림 (x좌표에 따라 y값이 밀림): [Sh_y =\begin{bmatrix}1 & 0 & 0 \b & 1 & 0 \0 & 0 & 1\end{bmatrix}\quad \text{(b: x가 클수록 y방향으로 많이 밀림)}]

---

🔹 점에 적용

점 ( (p_x, p_y) )에 대해: ( Sh_x \cdot p = (p_x + a \cdot p_y,\ p_y) )( Sh_y \cdot p = (p_x,\ p_y + b \cdot p_x) )

---

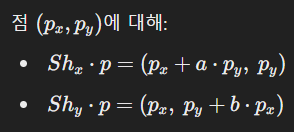
🔹 예시 해석

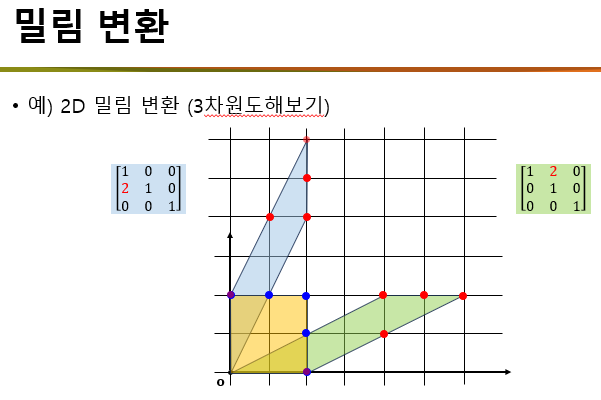
• 왼쪽 행렬: ( a = 2 ) → y좌표가 클수록 x방향으로 많이 밀림
• 오른쪽 행렬: ( b = 2 ) → x좌표가 클수록 y방향으로 많이 밀림

👉 노란색 삼각형이 각각 비스듬히 기울어진 평행사변형으로 변형됨!

---

✅ 3. 3D 밀림 변환

3D에서는 축이 3개(x, y, z)이므로, 총 6가지 방향으로 밀림이 가능합니다.

🔹 일반적인 3D 밀림 행렬

[ Sh_{3D} = \begin{bmatrix} 1 & sh_{xy} & sh_{xz} & 0 \ sh_{yx} & 1 & sh_{yz} & 0 \ sh_{zx} & sh_{zy} & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ]

항목	의미
( sh_{xy} )	y좌표에 따라 x방향으로 밀림
( sh_{xz} )	z좌표에 따라 x방향으로 밀림
( sh_{yx} )	x좌표에 따라 y방향으로 밀림
( sh_{yz} )	z좌표에 따라 y방향으로 밀림
( sh_{zx} )	x좌표에 따라 z방향으로 밀림
( sh_{zy} )	y좌표에 따라 z방향으로 밀림

---

🔹 예시: z축이 0이고 2D처럼 생각할 수 있는 경우

예:

[ Sh = \begin{bmatrix} 1 & 2 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} ]

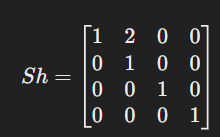
• y좌표가 클수록 x축 방향으로 더 많이 이동 → 비스듬히 누운 효과

---

✅ 4. 밀림 변환과 다른 변환과의 차이점

변환	크기 변화	각도 유지	평행성 유지
스케일	있음	유지 안 됨	유지됨
회전	없음	유지됨	유지됨
밀림	없음	유지 안 됨	유지됨 ✅

👉 밀림은 평행 구조는 유지되지만, 각도와 모양은 변형됩니다.

---

✨ 정리

항목	내용
정의	기준축에 따라 물체가 기울어지는 변환
2D	x, y축 밀림 (a, b 계수)
3D	xy, xz, yx, yz, zx, zy 방향 총 6종
특징	길이·각도는 변하지만, 직선성과 평행성은 유지
응용	기울어진 텍스트, 아이소메트릭 뷰 연출 등