🔁 2장 이론 (4): 정책 개선, 정책 반복, 그리고 가치 반복
🧭 정책 개선 (Policy Improvement)
정책 개선이란?
정책 개선은 현재 정책에 따라 계산된 상태가치 ( V_π(s) ) 를 기반으로,
각 상태에서 가장 높은 행동가치 ( Q_π(s,a) ) 를 갖는 행동을 선택해 새로운 정책으로 바꾸는 과정이다.

π*(s) = argmaxₐ Q_π(s, a)argmax는 가능한 행동 중 행동가치가 가장 큰 행동을 선택- 최적의 행동만을 선택한 것이 최적 정책 π*
정책이 변경되지 않으면 개선이 완료된 것으로 보고, 반복을 종료
🔄 정책 반복 (Policy Iteration)
Prediction과 Control
- Prediction: 현재 정책 π를 이용해 상태가치 ( V_π )를 계산하는 과정 (정책 평가)
- Control: 계산된 가치에 따라 정책을 개선하는 과정 (정책 개선)
정책 반복은 이 둘을 교대로 반복하여 최적 정책과 최적 상태가치를 찾아가는 방법
📜 정책 반복 알고리즘 요약
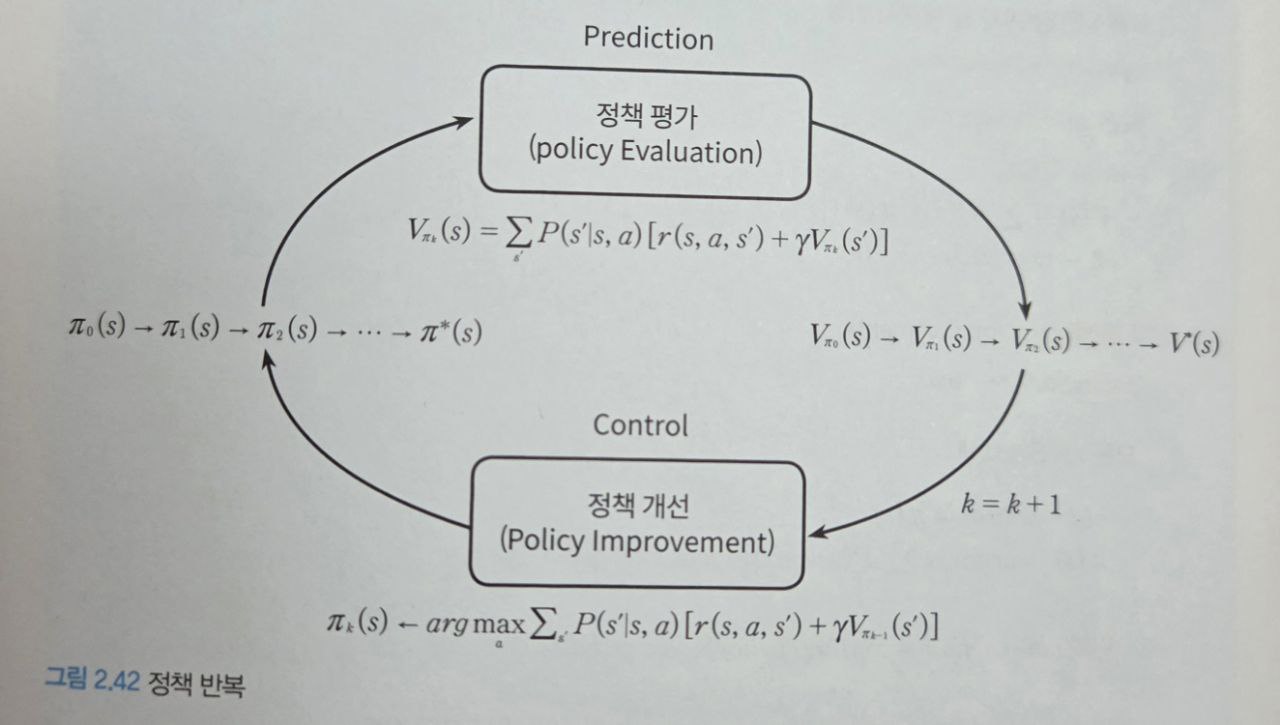
- Prediction에서는 정책 평가를 이용해 모든 상태의 상태가치 V_{π_0}(s) 계산
- Control에서는 상태가치 V_{π_0}(s0)를 이용해 정책 π_0(s)를 π_1(s)로 개선
- Prediction에서는 정책 평가를 이용해 모든 상태의 상태가치 V_{π_1}(s) 계산
- Control에서는 상태가치 V_{π_1}(s)를 이용해 정책 π_1(s)를 π_2(s)로 개선
…(무수히 반복)
- 최적 상태가치, 최적 정책으로 수렴🧑💻 코드 구현: 정책 평가 & 정책 개선
알고리즘: 반복 정책 평가
1. 초기화
모든 s ∈ S에 대해 V(s) ∈ R과 π(s) ∈ A(s)를 임의로 설정
2. 정책 평가
Δ < θ(작은 양수)가 될 때까지 반복:
Δ <- 0
모든 s ∈ S에 대해:
v <- V(s)
V(s) <- ∑_{s'} P(s'|s, π(s)) [r(s,π(s),s') + γV(s')]
Δ <- max(Δ, |v-V(s)|)
3. 정책 개선
policyStable <- true
모든 s ∈ S에 대해:
old - action <- π(s)
π(s) <- argmax_a ∑_{s'} P(s'|s,a)[r(s,a,s') + γV(s')]
만약 old-action ≠ π(s)라면 policyStable <- False
만약 policyStable = true라면 V ≈ v*, π ≈ π* 반환; 아니면 2부터 반복코드 구현
def policy_evalution(env, agent, v_table, policy):
gamma = 0.9
while(True):
# Δ←0
delta = 0
# v←𝑉(𝑠)
temp_v = copy.deepcopy(v_table)
# 모든 𝑠∈𝑆에 대해 :
for i in range(env.reward.shape[0]):
for j in range(env.reward.shape[1]):
# 에이전트를 지정된 좌표에 위치시킨후 가치함수를 계산
agent.set_pos([i,j])
# 현재 정책의 행동을 선택
action = policy[i,j]
observation, reward, done = env.move(agent, action)
v_table[i,j] = reward + gamma * v_table[observation[0],observation[1]]
# ∆←max(∆,|v−𝑉(𝑠)|)
# 계산전과 계산후의 가치의 차이를 계산
delta = np.max([delta, np.max(np.abs(temp_v-v_table))])
# 7. ∆ <𝜃가 작은 양수 일 때까지 반복
if delta < 0.000001:
break
return v_table, delta
def policy_improvement(env, agent, v_table, policy):
gamma = 0.9
# policyStable ← true
policyStable = True
# 모든 s∈S에 대해:
for i in range(env.reward.shape[0]):
for j in range(env.reward.shape[1]):
# 𝑜𝑙𝑑−𝑎𝑐𝑡𝑖𝑜𝑛←π(s)
old_action = policy[i,j]
# 가능한 행동중 최댓값을 가지는 행동을 선택
temp_action = 0
temp_value = -1e+10
for action in range(len(agent.action)):
agent.set_pos([i,j])
observation, reward, done = env.move(agent,action)
if temp_value < reward + gamma * v_table[observation[0],observation[1]]:
temp_action = action
temp_value = reward + gamma * v_table[observation[0],observation[1]]
# 만약 𝑜𝑙𝑑−𝑎𝑐𝑡𝑖𝑜𝑛"≠π(s)"라면, "policyStable ← False"
# old-action과 새로운 action이 다른지 체크
if old_action != temp_action :
policyStable = False
policy[i,j] = temp_action
return policy, policyStable
# 정책 반복
# 환경과 에이전트에 대한 초기 설정
np.random.seed(0)
env = Environment()
agent = Agent()
# 1. 초기화
# 모든 𝑠∈𝑆에 대해 𝑉(𝑠)∈𝑅과 π(𝑠)∈𝐴(𝑠)를 임의로 설정
v_table = np.random.rand(env.reward.shape[0], env.reward.shape[1])
policy = np.random.randint(0, 4,(env.reward.shape[0], env.reward.shape[1]))
print("Initial random V(S)")
show_v_table(np.round(v_table,2),env)
print()
print("Initial random Policy π0(S)")
show_policy(policy,env)
print("start policy iteration")
# 시작 시간을 변수에 저장
start_time = time.time()
max_iter_number = 20000
for iter_number in range(max_iter_number):
# 2.정책평가
v_table, delta = policy_evalution(env, agent, v_table, policy)
# 정책 평가 후 결과 표시
print("")
print("Vπ{0:}(S) delta = {1:.10f}".format(iter_number,delta))
show_v_table(np.round(v_table,2),env)
print()
# 3.정책개선
policy, policyStable = policy_improvement(env, agent, v_table, policy)
# policy 변화 저장
print("policy π{}(S)".format(iter_number+1))
show_policy(policy,env)
# 하나라도 old-action과 새로운 action이 다르다면 '2. 정책평가'를 반복
if(policyStable == True):
break
print("total_time = {}".format(time.time()-start_time))
📊 결과 해석: 그림 2.43 정책 반복

- 초기 정책은 랜덤한 방향으로 설정됨
- 정책 평가 → 정책 개선 반복 후, 정책은 점점 최적화됨
k=3에서 수렴하며, 모든 상태에서 도착지점으로 가는 최적 경로가 설정됨
🕒 전체 계산 시간은 약 0.2초로 매우 빠르며, 미로 크기가 작기 때문에 적은 반복 횟수로도 수렴함
🔁 가치 반복(Value Iteration)
📌 핵심 개념
가치 반복(Value Iteration) 은 정책 반복과 유사하지만, 다음과 같은 차이가 있다:
- 정책 반복은 정책 평가(Prediction)와 정책 개선(Control)을 분리해서 반복
- 가치 반복은 상태가치 함수 V(s)V(s)를 벨만 최적 방정식을 통해 반복적으로 업데이트하면서 동시에 정책 개선 효과를 포함
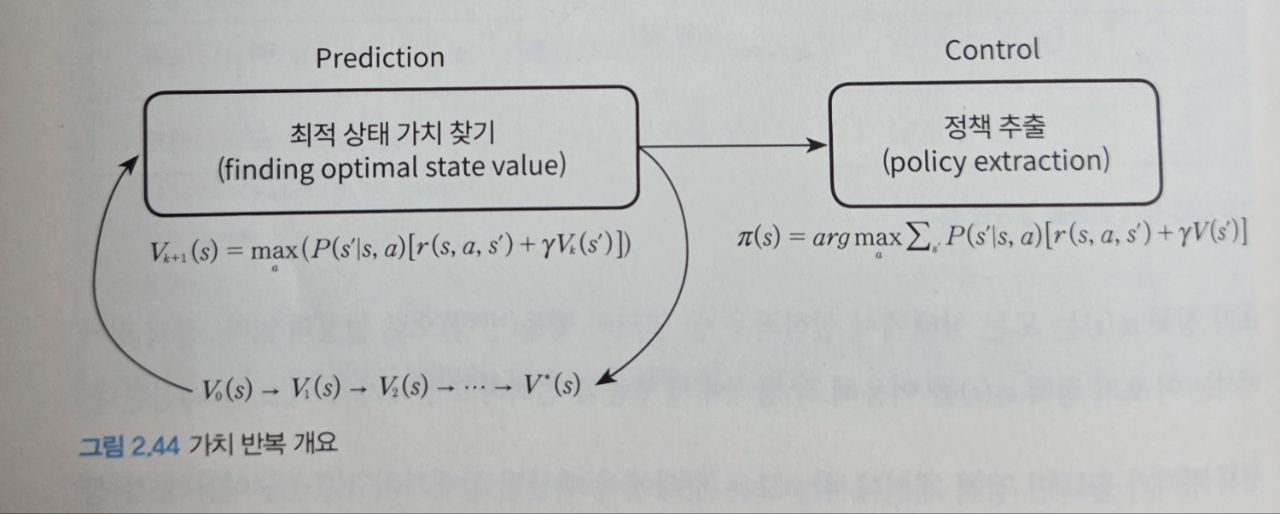
📎 그림 2.44는 전체 구조를 나타낸다. 가치 반복에서는 먼저 최적 상태가치를 찾고, 이후에 정책을 한 번만 추출한다.
가치 반복의 핵심 수식
상태가치 갱신 (Bellman 최적 방정식)
V_{k+1}(s) = max_a ∑_{s'} P(s'|s,a) [r(s,a,s') + γV_k(s')] # 식 2.21→ 현재 상태 s의 상태가치는, 가능한 모든 행동 a 중 최대 기대보상을 반환하는 a의 결과로 정의된다.
→ 정책 반복은 기대값의 합(E[Q])을 사용하지만, 가치 반복은 가능한 행동 중 가장 큰 값만 사용한다는 점이 다르다.
정책 추출
π(s) = argmax_a ∑_{s'} P(s'|s,a) [r(s,a,s') + γV(s')] # 식 2.22→ 수렴된 상태가치를 기반으로, 상태 s에서 가장 큰 행동가치를 주는 a를 선택하여 π(s)에 업데이트
🧾 알고리즘 요약
1. 초기화:
모든 s ∈ S^+에 대해 V(s)를 임의로 설정
2. 반복:
Δ ← 0
모든 상태 s ∈ S에 대해:
v ← V(s)
V(s) ← maxₐ ∑_{s'} P(s'|s,a)[r(s,a,s') + γV(s')]
Δ ← max(Δ, |v - V(s)|)
Δ < θ(작은 양수)가 될 때까지 반복
3. 정책 추출:
π(s) ← argmaxₐ ∑_{s'} P(s'|s,a)[r(s,a,s') + γV(s')]📘 코드 구현
def finding_optimal_value_function(env, agent, v_table):
k = 1
gamma = 0.9
while(True):
# Δ←0
delta=0
# v←𝑉(𝑠)
temp_v = copy.deepcopy(v_table)
# 모든 𝑠∈𝑆에 대해 :
for i in range(env.reward.shape[0]):
for j in range(env.reward.shape[1]):
temp = -1e+10
# print("s({0}):".format(i*env.reward.shape[0]+j))
# 𝑉(𝑠)← max(a)∑𝑃(𝑠'|𝑠,𝑎)[𝑟(𝑠,𝑎,𝑠') +𝛾𝑉(𝑠')]
# 가능한 행동을 선택
for action in range(len(agent.action)):
agent.set_pos([i,j])
observation, reward, done = env.move(agent, action)
# print("{0:.2f} = {1:.2f} + {2:.2f} * {3:.2f}" .format(reward + gamma* v_table[observation[0],observation[1]],reward, gamma,v_table[observation[0],observation[1]]))
#이동한 상태의 가치가 temp보다 크면
if temp < reward + gamma*v_table[observation[0],observation[1]]:
# temp 에 새로운 가치를 저장
temp = reward + gamma*v_table[observation[0],observation[1]]
# print("V({0}) :max = {1:.2f}".format(i*env.reward.shape[0]+j,temp))
# print()
# 이동 가능한 상태 중 가장 큰 가치를 저장
v_table[i,j] = temp
# ∆←max(∆,|v−𝑉(𝑠)|)
# 이전 가치와 비교해서 큰 값을 delta에 저장
# 계산전과 계산후의 가치의 차이 계산
delta = np.max([delta, np.max(np.abs(temp_v-v_table))])
# 7. ∆ <𝜃가 작은 양수 일 때까지 반복
if delta < 0.0000001:
break
# if k < 4 or k > 150:
# print("V{0}(S) : k = {1:3d} delta = {2:0.6f}".format(k,k, delta))
# show_v_table(np.round(v_table,2),env)
print("V{0}(S) : k = {1:3d} delta = {2:0.6f}".format(k,k, delta))
show_v_table(np.round(v_table,2),env)
k +=1
return v_table
def policy_extraction(env, agent, v_table, optimal_policy):
gamma = 0.9
#정책 𝜋를 다음과 같이 추출
# 𝜋(𝑠)← argmax(a)∑𝑃(𝑠'|𝑠,𝑎)[𝑟(𝑠,𝑎,𝑠') +𝛾𝑉(𝑠')]
# 모든 𝑠∈𝑆에 대해 :
for i in range(env.reward.shape[0]):
for j in range(env.reward.shape[1]):
temp = -1e+10
# 가능한 행동중 가치가 가장높은 값을 policy[i,j]에 저장
for action in range(len(agent.action)):
agent.set_pos([i,j])
observation, reward, done = env.move(agent,action)
if temp < reward + gamma * v_table[observation[0],observation[1]]:
optimal_policy[i,j] = action
temp = reward + gamma * v_table[observation[0],observation[1]]
return optimal_policy
# 가치 반복
# 환경, 에이전트를 초기화
np.random.seed(0)
env = Environment()
agent = Agent()
# 초기화
# 모든 𝑠∈𝑆^+에 대해 𝑉(𝑠)∈𝑅을 임의로 설정
v_table = np.random.rand(env.reward.shape[0], env.reward.shape[1])
print("Initial random V0(S)")
show_v_table(np.round(v_table,2),env)
print()
optimal_policy = np.zeros((env.reward.shape[0], env.reward.shape[1]))
print("start Value iteration")
print()
# 시작 시간 변수에 저장
start_time = time.time()
v_table = finding_optimal_value_function(env, agent, v_table)
optimal_policy = policy_extraction(env, agent, v_table, optimal_policy)
print("total_time = {}".format(np.round(time.time()-start_time),2))
print()
print("Optimal policy")
show_policy(optimal_policy, env)🧪 결과 분석 (📎 그림 2.45)

- 초기값 설정: 상태가치는 임의의 값으로 초기화됨.
- 상태 s₀ 계산 예시 (V₁(s₀))
- up = -3.00 + 0.9×0.55 = -2.51 right = -1.00 + 0.9×0.72 = -0.36 ← 선택 down = -1.00 + 0.9×0.54 = -0.51 left = -3.00 + 0.9×0.55 = -2.51
- 가장 큰 값인 right 방향의 -0.36이 V₁(s₀)에 저장됨.
- 총 반복 수: k = 153에서 수렴.
- 계산 시간: 약 1초 미만, 매우 빠름.
📎 정책 추출 결과는 정책 반복 알고리즘과 동일하게 도착지점으로 향하는 방향으로 수렴함.
'독서 > 기초부터 시작하는 강화학습 신경망 알고리즘' 카테고리의 다른 글
| 6. 몬테카를로 Control (0) | 2025.04.11 |
|---|---|
| 5. 몬테카를로 Prediction (0) | 2025.04.02 |
| 4.1 정책 평가와 반복 정책 평가 (0) | 2025.03.31 |
| 3.2 가치함수: 행동 가치 계산 (0) | 2025.03.31 |
| 3.1 가치함수: 상태 가치 계산 (0) | 2025.03.29 |